2020年8月26日追記
「令和2年対策で総括問題を追加しました」
2019年8月27日追記
「問題の解説を追加しました」
「変圧器の容量に関する計算問題」

本記事では「変圧器の容量、力率改善に関する計算」をマスターして頂く。
「力率」という言葉はご存じだろうか。
発電機、電動機、変圧器には運転曲線があって「cosθ」という力率により出力が決まる。当然、力率が1であるのが理想だ。
皮相電力を全て有効電力として活用できるからだ。
しかし、実際そうはいかない。
系統にぶらさがる負荷がモータでコイルだったり、送電線が容量性負荷であり、抵抗成分だけではないからだ。
それらを補うように発電機は無効電力を供給しなくてはいけない。
また、コンデンサを並列に設置するといった力率改善方法もある。変圧器と一緒に出題されるのはこっちの方だ。
力率改善がどういったものか、問題を解く中で学んで欲しい。
使う公式を整理する
①皮相電力の公式
下記のベクトル図が基本となる。これが一番分かりやすい。

問題では、力率角(θ)の影響でこういった図になることもある。(遅れ力率の場合)

②有効電力の公式
P=EIcosθ
③無効電力の公式
Q=EIsinθ
④三角関数の基本公式
三角関数の基本公式の一つだ。

さらに、問題でよく使うのは下記の式だ。
予め、式の展開に慣れておくといい。

変圧器の力率改善問題
この分野の出題問題のパターンは複数ある。視点を変えてくるのが厄介だが、公式のどこを求めに行くかを見極めることができれば解くことができるだろう。
過去問をみてみると
・電力用コンデンサの設置に関する問題
・負荷を追加するので、変圧器の力率改善を図る問題
これらを経験しておこう。
問題①
負荷(20000kV・A、遅れ力率90%)に電力供給している変電所があるとき、負荷と並列に4000kvarのコンデンサを設置した場合、変圧器の運転力率は何%となるか。
解説
この問題で重要なのが
「遅れ」と「進み」の知識である。問題を解く中で、コンデンサの投入はどう影響するのか理解しよう。
並列コンデンサを設置した後の無効電力量がわからない状態だ。
つまり、並列コンデンサを設置する前の無効電力が鍵になることがこの時点でわかる。
変圧器の運転力率を求めるので
①並列コンデンサ設置前の無効電力を求める
②追加するコンデンサ分を①から引いてやる
③有効電力量は変わらないので、②を使って皮相電力を求めて、力率を求める
これが解く流れだ。
①並列コンデンサ設置前の無効電力
Q=S× sinθ を使う。
力率は0.9であるからsinθは
sinθ=√(1-(0.9)^2)=0.436
従って、20000×0.436=8720[kVA]
②並列コンデンサ設置後の無効電力
①にて8720の遅れ電力があることが分かった。
遅れとはコイル成分のことである。
並列コンデンサを回路に追加するということは
8720ー4000=4720[kVA]
これが並列コンデンサ追加後の無効電力である。だんだんゴールが見えてきた。
③有効電力を求める
20000×0.9=18000[kW]
これは負荷に供給するものなので、力率が変わろうとも変化しない。
混乱しがちなのだが
むしろ、力率を変えようと「並列コンデンサを投入している」のである。(※必要あれば解説追加しますね。)
④運転力率を求める
ここまでの計算で
・有効電力
・無効電力
を求めることができた。
従って、皮相電力は
有効電力の2乗 と 無効電力の2乗 を足してルートを取ったものなので
S=(18000)^2 + (4720)^2
S=18608.6[kVA]
運転力率は18000/18608.6 ×100=96.7[%]
問題②
ある配電線に負荷(80kW、遅れ力率0.8)が接続しているとき、力率改善用の電力用コンデンサを接続したところ、線路損失が20%を減少させることができた。接続した電力用コンデンサの大きさはいくらか。負荷の電圧は一定とする。
解説
この問題で厄介なのは「比」だ。
ここを処理できるかどうかで決まる。
この問題で最終的に求めなくていけない答えが
「追加接続したコンデンサの大きさ」
この手の問題は大抵2パターンだ。
「コンデンサ接続後の皮相電力を求める」
「コンデンサ接続後の無効電力を求める」
今回与えられている情報だと、皮相電力を求めるしかない。
「皮相電力は線路損失の2乗に比例する」については機械科目で学習したと思うが、理解できているだろうか?※
(※もし、必要なら追加します)
2019年8月27日追記
簡潔にまとめましたので、活用頂ければと思います。
銅損(線路損失)が皮相電力の2乗に比例する理由 - 電験法規完全攻略
線路損失は抵抗の損失であるので「有効電力」であることを念のため、伝えておく。
では、実際に解いていく。
まず、前提条件を書いておく。
<コンデンサ追加前>
皮相電力をS1
有効電力をP1
<コンデンサ追加後>
皮相電力をS2
有効電力をP2
<問題文からわかること>
「有効電力80kWと力率0.8」の記載から皮相電力S1が100[kVA]、無効電力が60kvarであることがわかる。
有効電力P2は問題文から「P1×0.8」であることがわかる。
これまでの情報から下記の式を立てることができる。
P2/P1=(S2)^2 /(S1)^2
「P2=P1×0.8」を代入すると
S2=100×√0.8
S2=89.44[kVA]を求めることができる。
コンデンサ追加後の皮相電力を求めることができれば、「皮相電力S2の2乗」から「有効電力の2乗」を引いて、無効電力Q2も求めることができる。
「S2の2乗」=89.44×89.44=7999.51
「有効電力の2乗」=80×80=6400
Q2=40[kvar]
Q1ーQ2をすることで、追加したコンデンサ容量を求めることができる。
よって、60-40=20[kvar]
続いてはこの無効電力を補填する分野の総集編的な問題を共有する。是非とも挑戦してみて欲しい。
問題③
難易度が高いとされている平成24年の問12だ。
これは知識の網羅性を確かめるのに良い問題である。
問題文をよく読んでおこう
最近の電験はとにかく文字数が多い。見るだけでやる気をなくしてしまいそうになるが、これは慣れで解消することができる。決まった用語が並ぶにしか過ぎないので慣れてしまえば「スッ」と読めるようになる。逆にあまり見かえない言葉ばかりの文章を読むのは非常に疲れる。
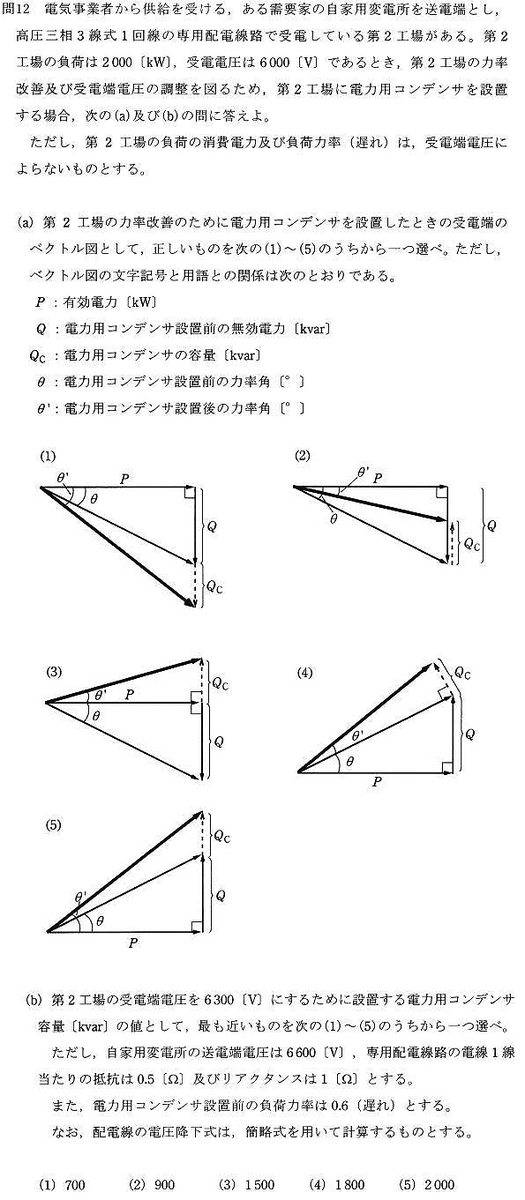
電気事業者から供給を受ける,ある需要家の自家用変電所を送電端とし,高圧三相 3 線式 1 回線の専用配電線路で受電している第 2 工場がある。第 2 工場の負荷は 2000 [kW] ,受電電圧は 6000 [V] であるとき,第 2 工場の力率改善及び受電端電圧の調整を図るため,第 2 工場に電力用コンデンサを設置する場合,次の(a)及び(b)の問に答えよ。
ただし,第 2 工場の負荷の消費電力及び負荷力率(遅れ)は,受電端電圧によらないものとする。
(a) 第 2 工場の力率改善のために電力用コンデンサを設置したときの受電端のベクトル図として,正しいものを次の(1)~(5)のうちから一つ選べ。ただし,ベクトル図の文字記号と用語との関係は次のとおりである。
(b) 第 2 工場の受電端電圧を 6300 [V] にするために設置する電力用コンデンサ容量は [kvar] の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,自家用変電所の送電端電圧は 6600 [V] ,専用配電線路の電線 1 線当たりの抵抗は 0.5 [Ω] 及びリアクタンスは 1 [Ω] とする。また,電力用コンデンサ設置前の負荷力率は 0.6 (遅れ)とする。なお,配電線の電圧降下式は,簡略式を用いて計算するものとする。
(1) 700 (2) 900 (3) 1500 (4) 1800 (5) 2000
解説
この問題は(a)は基礎知識を問う問題だ。
しかし(b)問題 は電力科目の知識(配電知識)を問うような問題となっている。実に最近の電験らしいと言える。3相の電線の電圧降下の式を忘れてしまっては解けない問題なのである。(エンジニアとして知っておかないといけない知識ということなのかもしれない)
(a)について
この問題で意地悪なのが「遅れ」「進み」という記載がない所である。これは「電力用コンデンサ」はどんな機能を持つのかを問いていると言えるだろう。
答えを言うと(2)が正しい。
まず基準としては、電力用コンデンサは「無効電力」に対してしか変動を与えることができない設備ある。つまり、縦軸にしか影響を与えることができないのだ。
そして、コンデンサは遅れ電力を補償し、進み側に移動させるという特性から(2)が正しい挙動であると判断することができる。
(b)について
まとめ
以上「過去問を20日で攻略「変圧器の容量問題」(5日目)」の記事になります。
この記事では
コンデンサの投入で「運転力率を「遅れ」から進み側に戻す」ことができる
このことを計算問題から学んで欲しいです。
当然、穴抜け問題でも出題される分野なので、役立つ知識になるでしょう。何回か解いて、計算の流れを理解・習得して、得点源にしてもらえればと思います。